Turtle Programming

Introduction

In this tutorial we will have a look at Turtle Programming. In 1967 a general purpose programming language called LOGO was created. The main highlight of this language was turtle graphics. In turtle graphics we have a robot with a pen which draws on a canvas. We can control this turtle using a few commands. The main commands are :

forward : move the turtle forward
turn : turn the turtle
penUp/penDown : activate/deactivate the turtle's pen

To get a brief understanding of how this works head over here.

While Turtle programming generally refers to a 2-D turtle we have a 3-D version available. In the 3-D version we have three types of turn available for each of the dimensions of the turtle.

pitch
yaw
roll

Let's first start with only operating on a 2-D plane and later we will discuss 3-D.

You need to clear up space for experimentation. Use setBlocks() with PiCraft.AIR to clear up space. If you are on the Java edition then it is suggested that you use New World -> Creative -> World Type: Superflat -> Customize -> Presets -> The Void -> Create New World Then we can setup a canvas for drawing as follows:

using PiCraft
p = getPos()
setBlocks(p .+ (-50, 0, -50), p .+ (50, 0, 50), Block(35, 15))

To initialize the turtle:

t = turtle(pos = p)

Since we are only concerned with the 2 dimensions of the plane we only need a single turn function which will be yaw

turn = yaw

move(t, 10)
turn(t, 45) # Note that the angle is in degrees, use `deg2rad(θ)` to convert from radians.
move(t, 10)
t.penBlock = PiCraft.IRON_BLOCK # Change penBlock
move(t, 10)
turn(t, 45)
move(t, 10)
t.penDown = false
turn(t, 90)
move(t, 10)
t.penDown = true
move(t, 10)

To reset the canvas and the turtle it can be convenient to define a function

function clrscr(t, p)
    setBlocks(p .+ (-50, 0, -50), p .+ (50, 0, 50), Block(35, 15))
    t.pos = p
end
clrscr(t, p)

Draw a square

move(t, 10)
yaw(t, 90)
move(t, 10)
yaw(t, 90)
move(t, 10)
yaw(t, 90)
move(t, 10)

We can also use a 'for loop' for the same

clrscr(t, p)
for i in 1:4
    move(t, 10)
    yaw(t, 90)
end

Similarly, we can draw a triangle

Draw a triangle

clrscr(t, p)
for i in 1:3
    move(t, 10)
    turn(t, 120)
end

Challenge: Figure out how to draw a general polygon using a loop

Solution:

function drawPolygon(t::turtle, n::Integer, l::Real)
    θ = 180 - 360/n
    for i in 1:n
        move(t, l)
        yaw(t, θ)
    end
end

clrscr(t, p)

Star

for i in 1:5
    move(t, 50)
    turn(t, 144)
end

We can also make spirals.

Spiral

clrscr(t, p)
for i in 1:10
    move(t, 5*i)
    turn(t, 90)
end

clrscr(t, p)
for i in 1:10
    move(t, 5 + 5*i)
    turn(t, 120)
end

3-D turtle

As mentioned earlier instedad of a single turn command we have 3 commands, namely yaw, pitch and roll.

In essence we have 3 mutually perpendicular axis on the turtle.

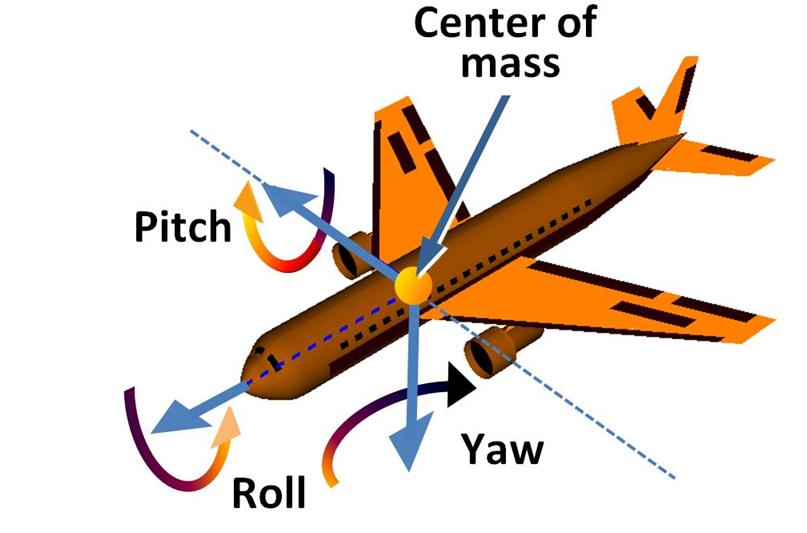
Longitudinal(turtle.direction, points forward) : Roll Axis
Lateral : Pitch Axis
Vertical(turtle.normal, points downwards) : Yaw Axis

To get the positive rotation direction use the corkscrew rule. corkscrew rule image

Curl your right hand's fingers with the thumb pointing outwards like in a thumbs up position. When your thumb points in the axis vector then the curl direction is the positive rotation direction.

We dont need a canvas to experiment with the 3-D turtle. Reset the world as required.

move(t, 10)
pitch(t, 45)
move(t, 10)
pitch(t, -45)
yaw(t, 90)
move(t, 10)
roll(t, 90)
pitch(t, 90)
move(t, 10)

We can use the same concepts of the 2-D turtle to draw in 3-D.

Square inclined at 45 degrees

t = turtle(pos = getPos())
pitch(t, 45)
for i in 1:4
    move(t, 10)
    yaw(t, 90)
end

Spring

t = turtle(pos = getPos())
R = 20
C = 2*pi*R
for i in 1:720
    move(t, C/90)
    yaw(t, 7)
    pitch(t, 5)
end

This page was generated using Literate.jl.